What Happens When Things Go Near the Speed of Light?

Advanced Analysis: Deriving the formula for g

Challenge Home - Online Resources - Challenge - Assessment - Site Index

Use the mathematical form of the plot to derive g.

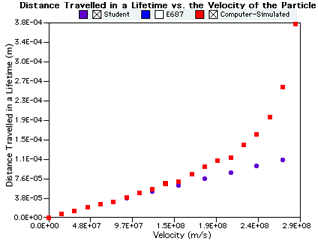Now, back to your first plot. Remember: Ty x g = To

We can understand the discrepancy because the larger the relative velocity between the two observers, the larger the disagreement in the times they measure.

What happens when the observer and the observed are traveling in the same frame of reference? This means that their relative velocity is 0, and therefore g will be 1. That is what is should be; both observers are in the same frame of reference, so no corrections are needed! When the velocity between observers is not zero, g > 1. When velocity is small compared to the speed of light (such as in everyday situations), g is close to 1, and the correction factor is insignificant.

What has your advanced analysis shown?